Геометрическая задача на доказательство HD
База анкет репетиторов по математике http://www.virtualacademy.ru/repetitory/po-matematike/ В данном уроке демонстрируется пример решения геометрической задачи, которым можно с успехом воспользоваться в качестве подготовки к ОГЭ по математике. Условие задачи для наглядности изображается схематически на рисунке. Для решения задачи производятся дополнительные построения: проводятся медианы OA и CK к боковым сторонам AB и BC соответственно. Следует отметить, что медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Значит, верны равенства CO=OB и AK=BK. Далее в ходе решения доказывается, что треугольники AOC и AKC равны по первому признаку равенства треугольников. Значит, равны и медианы OA и CK, что и требовалось доказать.
 HD
HD
 HD
HD HD
HD HD
HD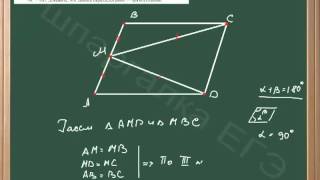
 HD
HD
 HD
HD
 HD
HD HD
HD HD
HD
![Доказательство 2=0 [MindYourDecisions на русском]](https://i.ytimg.com/vi/SzCmOsk2ZaQ/mqdefault.jpg) HD
HD

 HD
HD
 HD
HD HD
HD